elektrische Filter aus aktiven Bauteilen

Übersicht

• Tiefpass 1. Ordnung
• Hochpass 1. Ordnung
• Tiefpass 2. Ordnung nach Sallen-Key
• Tiefpass 2. Ordnung mit MLF
• Hochpass 2. Ordnung nach Sallen-Key
• Hochpass 2. Ordnung mit MLF
• Bandpass 2. Ordnung nach Sallen-Key
• Bandpass 2. Ordnung mit MLF
• Doppel-T-Bandsperre
• Doppel-T-Bandsperren Variante
• Fliege-Filter als Bandsperre
• Quellen

Auf umliegenden Seiten habe ich…
Spannungsteiler und passive Filter
  TP, HP, BP, BS, AP, Doppel-T, Wien-Brücke, etc.
allgemeine OP-Schaltungen   Addierer, Subtrahierer, Instrumenten-Verstärker,
  Integrator, Differenzierer, NIC, Gyrator, Oszillator, etc.
aktive Filter nach Charakter und Aufbau   Güte, Dämpfung,
  Tschebyscheff, Cauer, Butterworth, Legendre, Bessel, Thomson,
  FIR, Nyquist, Raised-Cosine, RRC, Gauß,
  IIR, Sallen-Key, MLF, Linkwitz-Riley, etc.
spezielle Filter   Equalizer, BiQuad, State Variable, etc.
 

Aktive Filter haben viele Vorteile:

• Spulen können vermieden werden, welche bei tiefen Frequenzen teuer,
  schlechte elektrische Parameter haben und großvolumig sind.
• Durch entsprechende Schaltungsauslegung können kleine Kondensatoren verwendet werden.
• Trotz ca. 10% ungenauer Kondensatoren, können genaue Filter mittels Poti aufgebaut werden.
• Potis können durch FETs oder Digital-Potis ersetzt werden.
• Je nach Amplitude, lassen sich die Filtereigenschaften einstellen (z.B. Loudness)
• Die Filtereigenschaften sind nicht abhängig von der Last (z.B. Lautsprecherimpedanz)
• Mit aktiven Komponenten z.B. OP's lassen sich auch negative Widerstände realisieren
  → Dämpfung D < 0 → Oszillatoren sind möglich.

Tiefpass 1. Ordnung

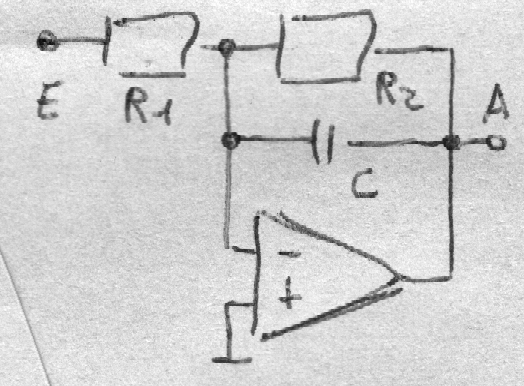
V = - (R₂ || 1/jωC) / R₁ = - R₂ / (R₁ (1 + jωR₂C) )

Mit folgenden Gleichungen ergibt sich die allgemeine Form.

ω₀ = 1/(R₂C) = 1 / T;   R₂/R₁ = k   und   jω + δ = s

V = - k / (1 + jω/ω₀) = - k / (1 + Ts)

Alternativ, kann ein passiver RC-Tiefpass aufgebaut werden,
welcher dann von einen hochohmigen positiven Verstärker gepuffert wird.

Zum Anfang

Hochpass 1. Ordnung

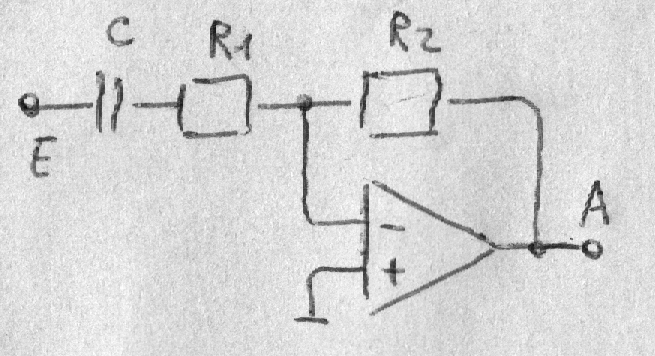
V = - R₂ / (R₁ + 1/jωC) = - jωR₂C / (1 + jωR₁C)

Mit folgenden Gleichungen ergibt sich wider die allgemeine Form.

ω₀ = 1/(R₁C)   und   - R₂/R₁ = k

V = k jω/ω₀ / (1 + jω/ω₀) = k Ts / (1 + Ts)

Siehe auch passiver RC-Hochpass oder passiver RL-Hochpass.

Zum Anfang

Tiefpass 2. Ordnung nach Sallen-Key

Die allgemeine Übertragungsfunktion eines TP₂-Systems lautet wie folgt.

G(s) = b₀ / ( a₂s² + a₁s + 1 )

Wenn die Güte nicht so hoch sein braucht
(ca. Q < 3 - hängt z.B. von Eckfrequenz & OP ab),
kann man den Tiefpass als Sallen-Key-Filter realisieren, wie hier dargestellt.

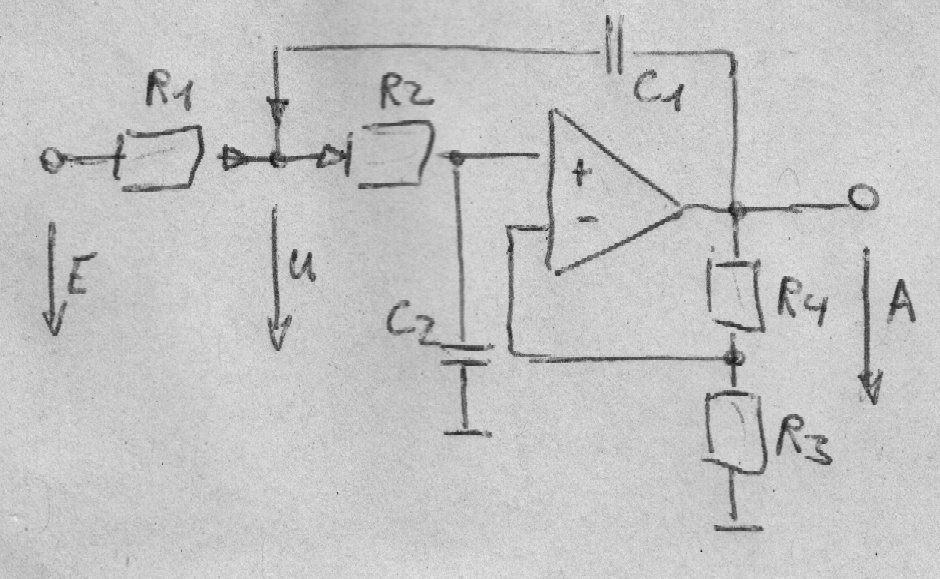
Über die Knotenregel erhalte ich…

(E - U) / R₁ + (A - U) / Z₁ - U / (R₂ + Z₂) = 0

→ E / R₁ = U / R₁ - A / Z₁ + U / Z₁ + U / (R₂ + Z₂)

Da die Spannungdifferenz der Eingänge des OPs = Null ist, folgt daraus…

U Z₂ / (R₂ + Z₂)   =   A R₃ / (R₃ + R₄)   mit   V = (R₃ + R₄) / R₃

→ U =   A (jωR₂C₂ + 1) / V

Dies oben eingesetz mit   Z₁ = 1 / jωC₁   bzw.   Z₂ = 1 / jωC₂   ergibt eine etwas sperrige Formel,
welche ich wieder eingescannt habe.

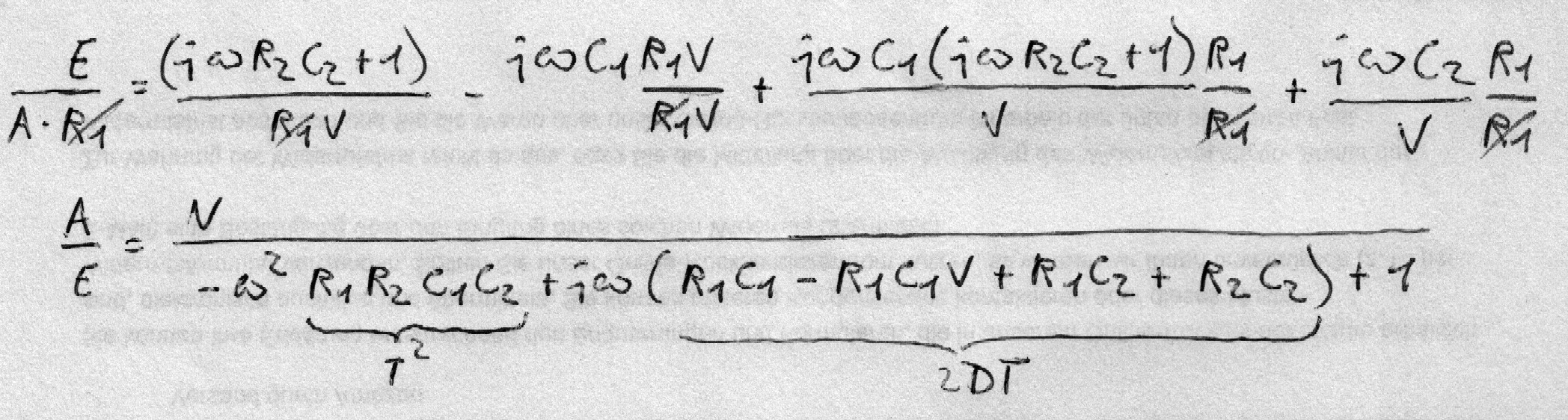
b₀ = V;   V = (R₃ + R₄ ) / R₃
a₂ = T² = R₁R₂C₁C₂
a₁ = 2DT = R₁C₁ - R₁C₁V + R₁C₂ + R₂C₂   Stabil für   R₁C₁ + R₁C₂ + R₂C₂ > R₁C₁V

Allgemeines Vorgehen

Aufgrund der gröberen Rasterung und Auswahl, wähle ich zunächst die Kondensatoren (im Bereich 1 nF… 680 nF).
Bei Werte darunter sollte die OP-Eingangs-Kapazität und evtl. die Leiterbahnkapazität mit berücksichtigt werden.
Werte darüber werden nicht nur unhandlich groß,
sondern deren Impedanz ist dann in der Größenordnung des Ausgangswiderstandes des OPs.

Danach berechne ich bei vorgegebener Eckfrequenz die Widerstände aus.
Sind diese außerhalb von z.B. 390 Ω…50 KΩ, fange ich wieder von vorne an.
Bei zu niedrigen Werten ist wieder mit einer Verfälschung durch den OP Ausgangswiderstand zu rechnen.
Bei zu hochohmigen Aufbau, ist Rauschen und der OP Eingangswiderstand ein Problem.

Abgesehen davon, ist der OP kein ideales Bauteil…
Das kann dazu führen, dass sowohl die Eckfrequenz alsauch die Dämpfung nicht erreicht werden.
Desweiteren, kann diese Schaltung schwingen.

Also oberhalb der "Resonanzspitze" sollte im Amplitudendiagramm noch eine Reserve
von ca. 40 dB (1% Fehler am OP Ausgang) sein,
berechenbar oder zeichenbar durch die Diagonale gebildet aus OP-Bandbreite und open-loop Verstärkung.
Um das zu überprüfen, ist es sinnvoll in einer Schaltungssimulation
(mit adäquaten OP-Modell) ein wenig mit den R & C Werten zu spielen.

Siehe z.B.
elektronikentwickler-aachen.de   Berechnung der Kapazität von Leiterbahnen
de.wikipedia.org   Ngspice
okawa-denshi.jp   Sallen-Key Low-pass Filter Design Tool

Widerstände und Kondensatoren beim Sallen-Key-TP gleich setzen

Ein Ansatz wäre, alle Widerstände und Kondensatoren gleich zusetzen.

→ T = RC   und   2DT = RC (3 - V) → V = 3 - 2D

Der Charakter des Filters ist dann offensichtlich nur vom Verstärkungsfaktor abhängig…

id="TP2skm"> Beim Sallen-Key-TP Spannungsteiler für Verstärkung entfernen

Ein weiterer Ansatz wäre, den Spannungsteiler, bestehend aus R₃ und R₄, zu entfernen.

→ V = 1   und   T² = R₁R₂C₁C₂   und   2DT = (R₁ + R₂) C₂

Zur weiteren Vereinfachung stelle ich mir vor, alle Widerstände und Kondensatoren sind zunächst gleich.
Nun kann ich durch "verstimmen" der Widerstände oder Kondensatoren meine Dämpfung beeinflussen
ohne das die Eckfrequenz driftet.
Also, kann ich erst einmal folgendes ansetzen.

SR₁ n = R = R₂ / n   bzw.   C₁ m = C = C₂ / m

Damit ergibt sich…   T = RC   und   D = m (1 + n² ) / 2n

bzw. nach   n   aufgelöst ergibt das

n² - 2Dn / m + 1 = 0   →   n_1,2 = D / m ± √(D² / m² - 1)

Da man weis, das sich die Dämpfung sinnvollerweise nur in einen bestimmten Bereich bewegt z.B.   0 < D < 1
…und man ein reales  n  möchte, sollte  D > m   sein.

Das lässt sich nur erreichen, wenn folgendes gegeben ist.   R₁ ≠ R₂   bzw.   n ≠ 1

Für beispielsweise   m² = 0,1   also   C₁ = 10 C₂   und   R₁ n = R = R₂ / n   bekomme ich folgende Tabelle.

Da   D > m   erforderlich ist, komme ich in diesem Beispiel für   C₁ = 10 C₂   nur bis etwa   D > 0,3162.
Sollte das nicht reichen, kann ich immer noch der Verhältnis der Kondensatoren vergrößern
Siehe letzte Spalte   C₁ = 100 C₂

Zum Anfang

Tiefpass 2. Ordnung mit MLF

Die allgemeine Übertragungsfunktion eines TP₂-Systems lautet wie folgt.

G(s) = b₀ / ( a₂s² + a₁s + 1 )

Benötige ich ein Filter höherer Güte oder
komme ich näher an das Bandbreiten Verstärkungs Produkt des OPs heran,
ist es besser etwas mehr Aufwand (ein Widerstand), als beim Sallen-Key-Filter, zu betreiben.

Der multible loop feedback - MLF-Filter ist damit fast immer stabil,
vorausgesetzt der OP kann hinreichend, als Ideal betrachtet werden…

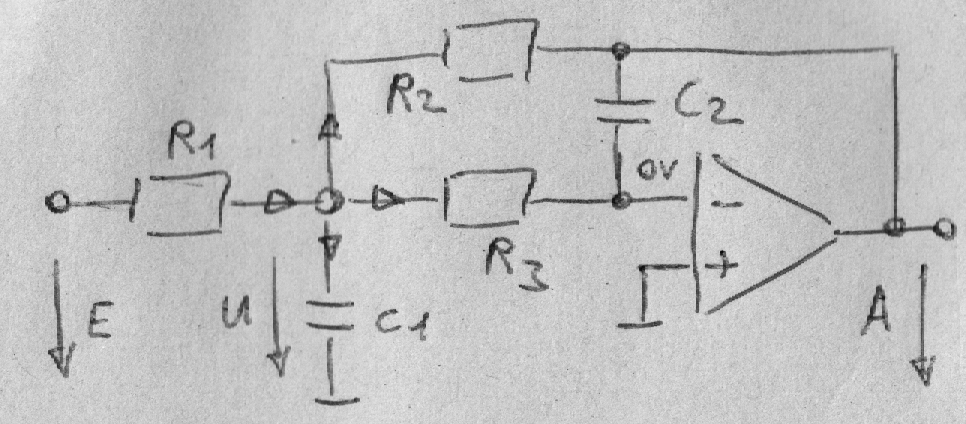
Da die Eingangsdifferenzspannung des OPs = 0 ist und kein Strom in den Eingang fließt, folgt.

U / R₃ = - A / Z₂

Und mit der Knotenregel erhalte ich…

(E - U) / R₁ = (U - A) / R₂ + U / R₃ + U / Z₁

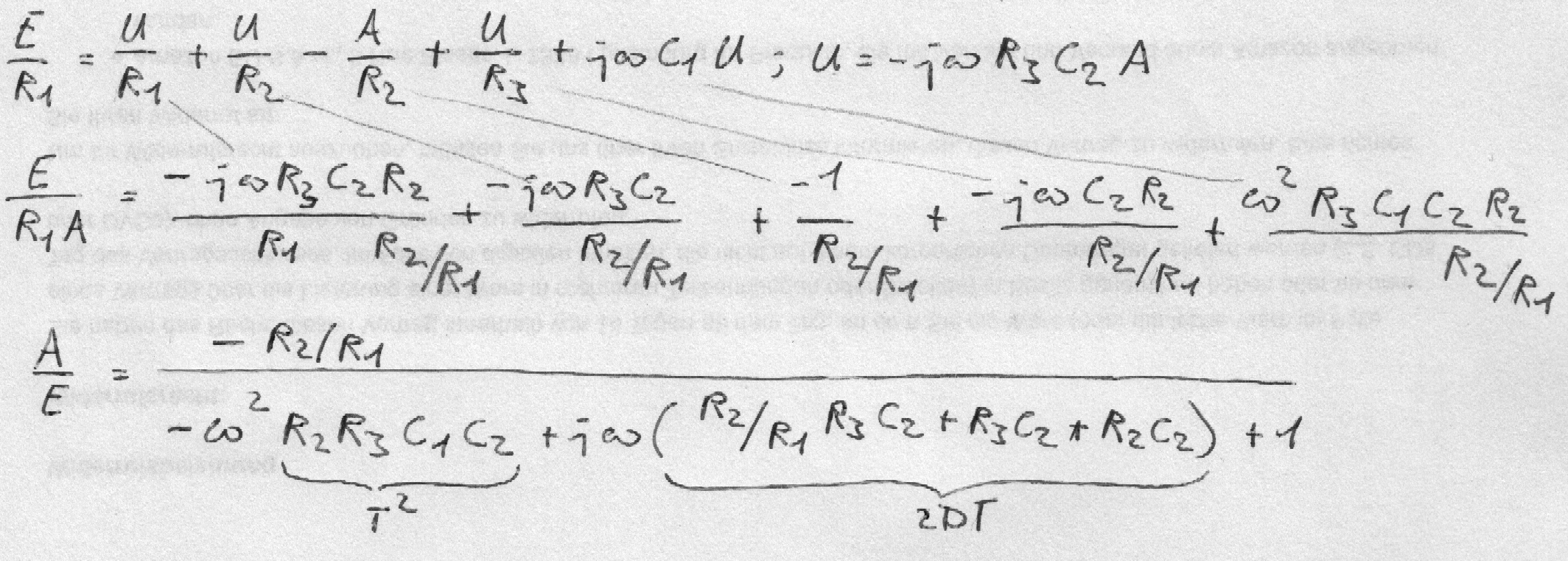
b₀ = V < 0;   Die DC-Verstärkung ergibt sich zu   V = - R₂ / R₁
a₂ = T² = R₂R₃C₁C₂   In T ist kein R₁ enthalten…
a₁ = 2DT = - V R₃C₂ + R₃C₂ + R₂C₂   Der Term   2DT   ist immer positiv bzw. stabil.

Zum Anfang

Teil der Widerstände beim MLF-TP gleich setzen

Ein Ansatz wäre, alle Kondensatoren und die Widerstände   R₂ = R = R₃   gleich zusetzen.

→ T = RC   und   2DT = (2 - V) RC → V = 2 - 2D

Für eine Dämpfung im Bereich   0 < D < 1   kommt da allerdings nur eine nicht realisierbare positive Verstärkung heraus…

Wenn ich allerdings erlaube die Kondensatoren zu "verstimmen", habe ich eine Chance auf eine Lösung.

Aus   C₁ m = C = C₂ / m   und   R₂ = R = R₃   ergibt sich folgendes   V = 2 - 2D / m

Für eine negative Verstärkungen muss   D > m   sein.

Wenn ich beispielsweise   m² = 0,1   setze, bekomme ich folgende Tabelle

Eine weitere Spreizung der Kondensatorenwerte macht wahrscheinlich keinen Sinn…

MLF-TP ohne DC-Verstärkung

Ein weiterer Ansatz wäre, die Gleichsetzung der Widerstände   R₁ = R = R₂.
Dadurch wird die DC-Verstärkung   V = - 1 = - R₂ / R₁ .

Das Verhältnis zum verbleibenden Widerstand bezeichne ich dann mit   R = R₃ / n²
bzw. das Verhältnis der Kondensatoren definiere ich zu   C₁ m = C = C₂ / m

→ T = RCn   und   2DT = (2n² + 1) RCm

→ D = (2n² + 1) m / 2n   oder   n² - Dn / m + 1 / 2 = 0   → n_1,2 = D / 2m ± √(D² / 4m² - 1 / 2 )

Für reale   n   sollte   D² > 2m²   sein.

Mit den Beispiel  m² = 0,1   also   C₁ = 10 C₂   und   R = R₃ / n²   folgt folgende Tabelle

Zum Anfang

Hochpass 2. Ordnung nach Sallen-Key

Durch vertauschen der Kondensatoren mit den Widerständen erhalte ich aus den PT₂ ein D²T₂-System.

G(s) = b₂s² / ( a₂s² + a₁s + 1 )

Die entsprechende Schaltung lässt sich beispielsweise als Sallen-Key Hochpass realisieren.

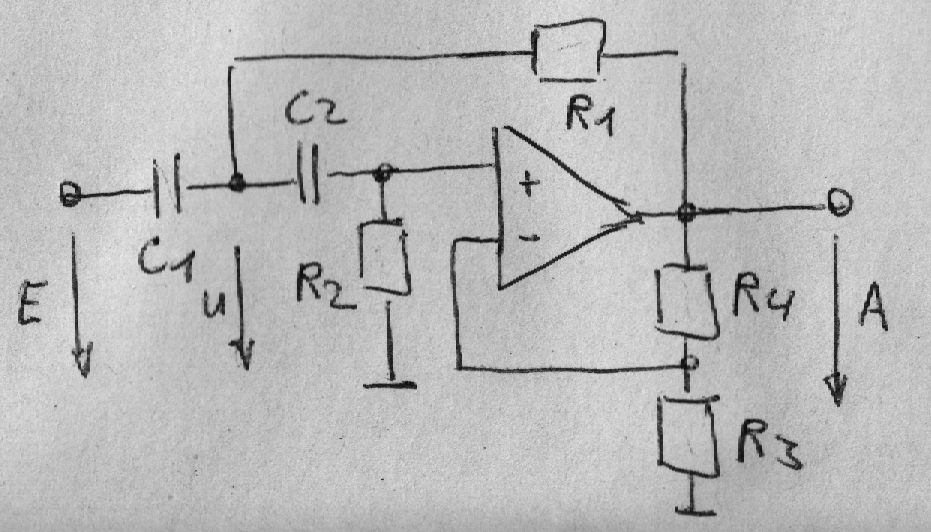
Im Vergleich zum Sallen-Key-Tiefpass ist die Konstante   2DT   leicht anders.

b₂ = a₂V;   V = (R₃ + R₄) / R₃
a₂ = T² = R₁R₂C₁C₂
a₁ = 2DT = R₁C₁ + R₂C₂ - R₂C₂V + R₁C₂

Beim Sallen-Key HP Widerstände und Kondensatoren gleich setzen

Für   R₁ = R = R₂   und   C₁ = C = C₂

bleibt nur noch veränderlich die Verstärkung   V = (R₃ + R₄ ) / R₃

→ T = RC   und   V = 3 - 2D

Weitere Schritte, wie beim Tiefpass 2. Ordnung nach Sallen-Key.

Beim Sallen-Key HP Verstärkung auf 1 setzen

Für eine AC-Verstärkung bei hohen Frequenzen   V = 1   und
Verstimmung der Widerstände oder Kondensatoren gemäß…

R₁n = R = R₂ / n   und   C₁m = C = C₂ / m

ergibt sich   → T = RC   und   D = (1 + m²) / 2nm

bzw. n = (1 + m²) / 2Dm = (1 + m²) Q / m

n   ist also immer positiv, egal wie   D   oder   m   ist.
Wenn ich beispielsweise   m² = 0,1   setze, bekomme ich folgende Tabelle.

Zum Anfang

Hochpass 2. Ordnung mit MLF

Durch vertauschen der Kondensatoren mit den Widerständen erhalte ich aus den PT₂ ein D²T₂-System.

G(s) = b₂s² / ( a₂s² + a₁s + 1 )

Den entsprechenden invertierenden Filter lässt sich auch in MLF - multible loop feedback Topologie realisieren.

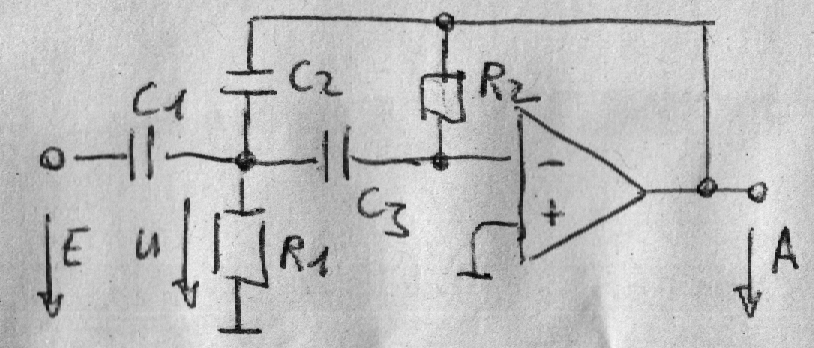
Im Vergleich zum MLF-Tiefpass ist die Konstante   2DT   ähnlich aufgebaut.

b₂ = a₂V
V = - C₁ / C₂
a₂ = T² = R₁R₂C₂C₃
a₁ = 2DT = R₁ (C₁ + C₂ + C₃) = R₁ (C₂ - VC₂ + C₃)

Beim MLF-HP Widerstände und ein Teil der Kondensatoren gleich setzen

Für   R₁ = R = R₂   und   C₂ = C = C₃   und   V = - C₁ / C

→ T = RC   und   V = 2 - 2D

Wie beim MLF-Tiefpass 2. Ordnung zu sehen, war keine negative Verstärkung für 0 < D < 1 möglich.

Weitere Schritte kann man sich aber sowiso ersparen,
da das Verhältnis der Kondensatoren C₁ / C₂ ,
welches die Verstärkung bestimmt, eh nicht in so einen feinen Raster,
wie Widerstände, zu bekommen ist.

Beim MLF-HP die AC-Verstärkung auf - 1 setzen

Durch gleichsetzen aller Kondensatoren   C₁ = C₂ = C₃ = C   wird die AC-Verstärkung für hohe Frequenzen   V = - 1

Wenn ich nun wieder folgende Abhänigkeit definiere   R₁ n = R = R₂ / n  bekomme ich folgendes.

→ T = RC   und   n = 3 / 2D

Damit ergibt sich dann folgende Tabelle:

Zum Anfang

Bandpass 2. Ordnung nach Sallen-Key

Um einen Bandpass zu erhalten, reicht es nicht mehr aus nur Kondensatoren mit Widerständen zu vertauschen.
Zumindest ist ein Bandpass ein DT₂-System mit folgender Gleichung.

G(s) = b₁s / ( a₂s² + a₁s + 1 )

Die entsprechende Schaltung lässt sich beispielsweise als Sallen-Key Bandpass wie folgt realisieren.

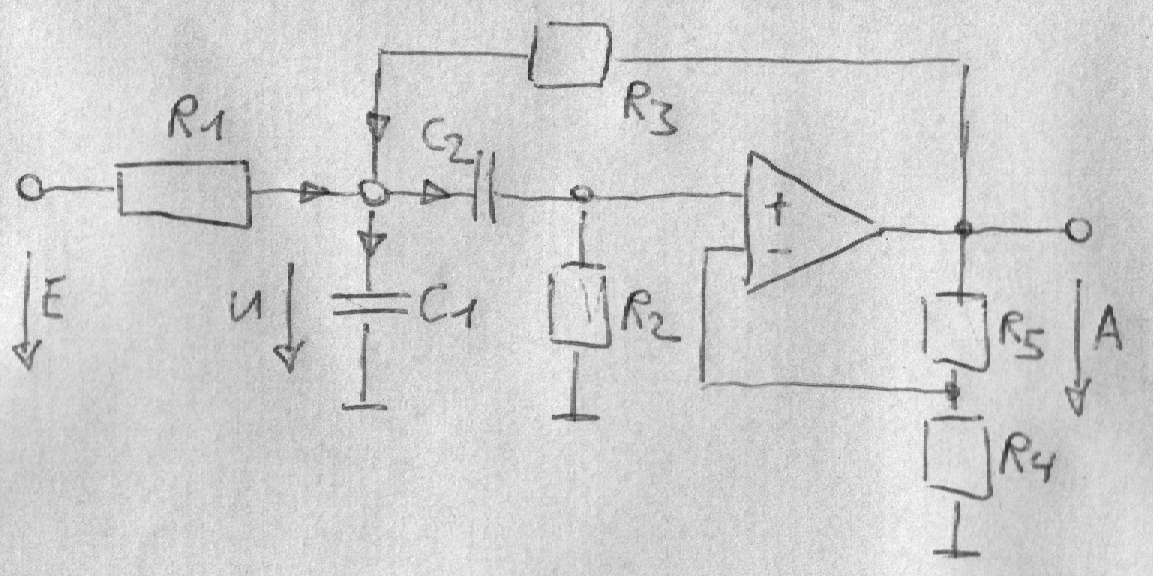
Im Vergleich zum Sallen-Key-Tiefpass ist die Konstante   2DT   gänzlich anders.

V = (R₄ + R₅) / R₄
b₁ = R₂C₂V   R₃ / (R₁ + R₃)
a₂ = T² = R₁R₂C₁C₂   R₃ / (R₁ + R₃)
a₁ = 2DT = (R₁R₃C₁ + R₁R₃C₂ + R₂R₃C₂ - R₁R₂C₂V + R₁R₂C₂)   / (R₁ + R₃)

Beim Sallen-Key-BP Widerstände und Kondensatoren gleich setzen

Für   R₁ = R₂ = R₃ = R   und   C₁ = C = C₂   und der Verstärkung   V = (R₄ + R₅ ) / R₄

ergibt sich…

→ T = √(2) RC / 2   und   4DT = (4 - V) RC   bzw.   V = 4 - 2D √2

Damit ergibt sich dann folgende Tabelle:

Zum Anfang

Beim Sallen-Key BP Verstärkung auf 1 setzen

Für   V = 1   und geschicktes Verstimmung der Widerstände oder Kondensatoren gemäß…

R₁ n = R₃ n = R = R₂ / n   und   C₁m = C = C₂ / m

erhält man…

→ T = √(2) RC / 2   und   2DT = RC (1 / (n m) + m / n + n m)

bzw.   n² - √(2) 2D n / m + 1 / m² + 1 = 0
→ n_1,2 = √(2) D / m ± √( 2 D² / m² - 1 / m² - 1)

Für   m² = 1   muß   D² > 1   sein, was uninteressant ist.
Wenn ich beispielsweise   m² = 0,1   oder   m² = 0,01   setze, bekomme ich folgende Tabelle

Zum Anfang

Bandpass 2. Ordnung mit MLF

Bei dem MLF-Bandpass wird die Schaltung, vergleichbar dem SK-Bandpass, auch ein wenig komplexer.
Allgemein ist ein Bandpass ein DT₂-System mit folgender Gleichung.

G(s) = b₁s / ( a₂s² + a₁s + 1 )

Der invertierende Filter lässt sich auch in MLF - multible loop feedback Topologie realisieren.

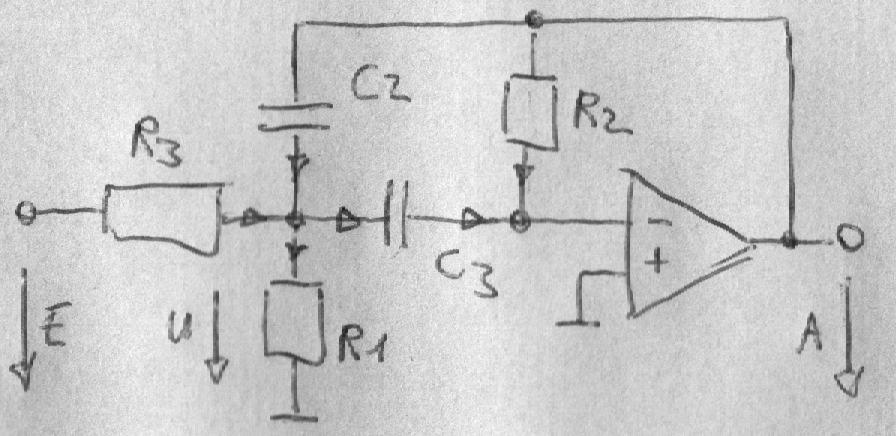
Im Vergleich zum SK-Bandpass sind die Konstanten ähnlich aufgebaut.

b₁ = - R₂C₃   × R₁ / (R₁ + R₃)
a₂ = T² = R₂R₃C₂C₃   × R₁ / (R₁ + R₃)
a₁ = 2DT = R₃ (C₂ + C₃)   × R₁ / (R₁ + R₃)

Beim MLF-BP Kondensatoren und ein Teil der Widerstände gleich setzen

Durch folgende Wahl lässt sich die Dämpfung ändern, ohne die Eckfrequenz zu ändern.

R₁ = R n;   R₂ = R (n +1) / n;   R = R₃   und   C₂ = C = C₃

Entsprechend kann man über die "Verstimmung" der Widerstände R₁ und R₂ die Dämpfung ändern.

→ T = RC   und   D = n / (n + 1) → n = D / (1 - D)

Zum Anfang

Doppel-T-Bandsperre

Bansperren via Hoch- und Tiefpass betrachte ich hier nicht…

Andere Bezeichnungen für eine Bandsperre sind Kerbfilter oder Notchfilter.
Allgemein ist eine Bandsperre ein PD²T₂-System mit folgender Gleichung.

G(s) = (b₂ s² + 1) / ( a₂ s² + a₁ s + 1 )

Die passive Bandsperre via Doppel-T-Filter hat noch den Nachteil der konstanten Dämpfung   D = 2.
Dies lässt sich durch Hinzunahme eines OPs verbessern.
Das grundsätzliche Problem der Toleranzen der Kapazitäten bleibt jedoch bestehen,
sodaß diese Schaltung kaum Anwendung findet.

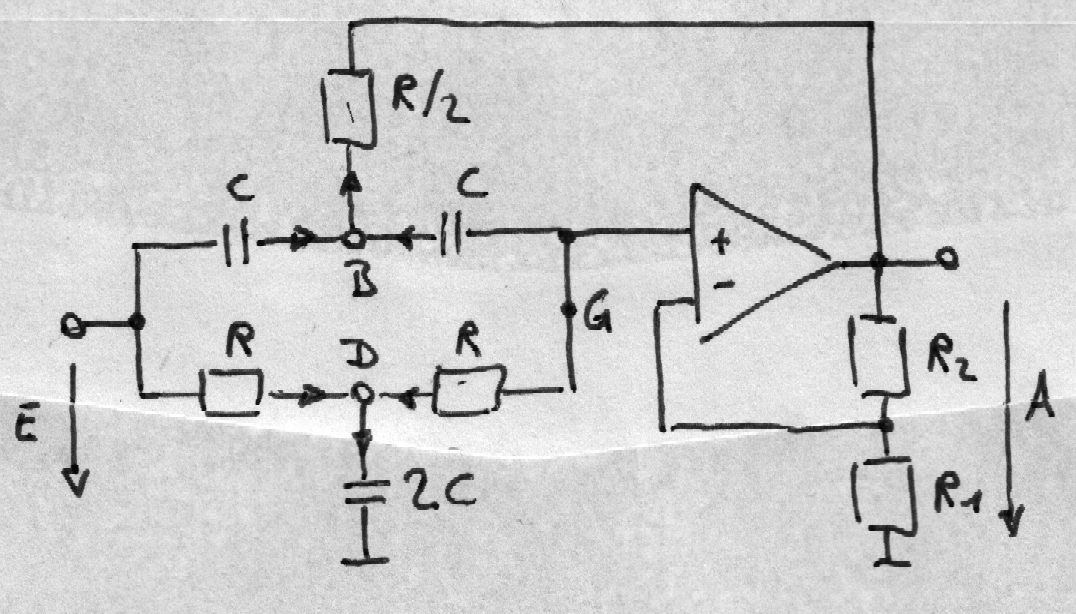
Die Berechnung erfolgt ähnlich wie bei der passiven Doppel-T-Bandsperre.

(E - B) jω C + (G - B) jω C = 2 (B - A) / R   →   jω RC E/2 + jω RC A / (2V) + A = B (1 + jω RC)

(E - D) / R + (G - D) / R = 2 D jω C       →   E/2 + A / (2V) = D (1 + jω RC)

(G - D) / R + (G - B) jω C = 0         →   (1 + jω RC) A/V - D - B jω RC = 0

A = G (R₁ + R₂) / R₁           →   G = A / V;     1 ≤ V < 2

Nun kann man die 1. und 2. Gleichung in die 3. einsetzen und
mit Hilfe der 4. Gleichung G durch A ersetzen und es folgt.

A / E = (1 - ω² R² C² ) V / ( - ω² R² C² + jω RC (4 - 2V) + 1 )

T = RC;   2DT = RC (4 - 2V)

Ein Verstärkung von   V = 2   ergibt theoretisch
(ideale Bauteile vorausgesetzt) keine Dämpfung.

Zum Anfang

Doppel-T-Bandsperre abgewandelt

Es gibt noch eine Variante, welche gegenüber der ursprünglichen Doppel-T-Bandsperre
nicht zu einer höheren Verstärkung bei höherer Güte führt.

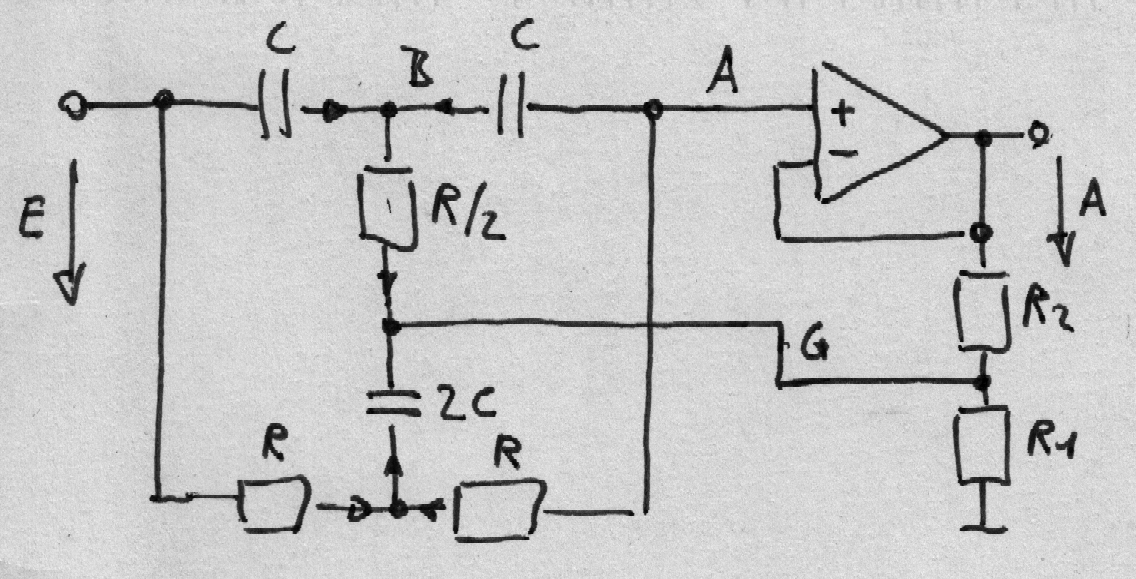
Die Berechnung erfolgt ähnlich wie bei der vorherige Doppel-T-Bandsperre.
V   ist hier jedoch statt eines Verstärkungsfaktors ein Teilerfaktor.

(E - B) jω C + (A - B) jω C + 2 (G - B) / R = 0   →   jω RC E/2 + jω RC A/2 + VA = B (1 + jω RC)

(E - D) / R + (A - D) / R = (D - G) jω 2C       →   E/2 + A/2 + VA jω RC = D (1 + jω RC)

(A - D) / R + (A - B) jω C = 0         →   D + B jω RC - A (1 + jω RC) = 0

Ist der Spannungsteiler, bestehend aus R₁ & R₂ niederohmig,
im Vergleich zur übrigen Schaltung, kann ich folgendes annehmen.

A R₁ / (R₁ + R₂) = G           →   A V = G     0 ≤ V ≤ 1

Nun kann man die 1. und 2. Gleichung in die 3. einsetzen und
mit Hilfe der 4. Gleichung G durch A ersetzen und es folgt.

A / E = (1 - ω² R²C² ) / ( - ω² R²C² + jω 4RC (1 - V) + 1 )

T = RC;   2DT = 4RC (1 - V) → V = 1 - D/2

Zum Anfang

Fliege-Filter als Bandsperre

Das grundsätzliche Problem, dass man beim Doppel-T-Filter möglichst identische Kondensatoren benötigt,
lässt sich umgehen, indem man eine RLC-Bandsperre mit einer virtuellen Induktivität aufbaut.
Die Bauteile R₁, C₂, R₃, R₄ und R₅ sind bewusst
wie bei der Schaltung für die virtuelle Induktivität gewählt worden
um eine Wiedererkennung zu erleichtern.

Im Normalfall regelt ein OP so aus, dass die Eingangsdifferenzspannung Null ist.
Entsprechend ist an 3 Punkten die gleiche Spannung D.

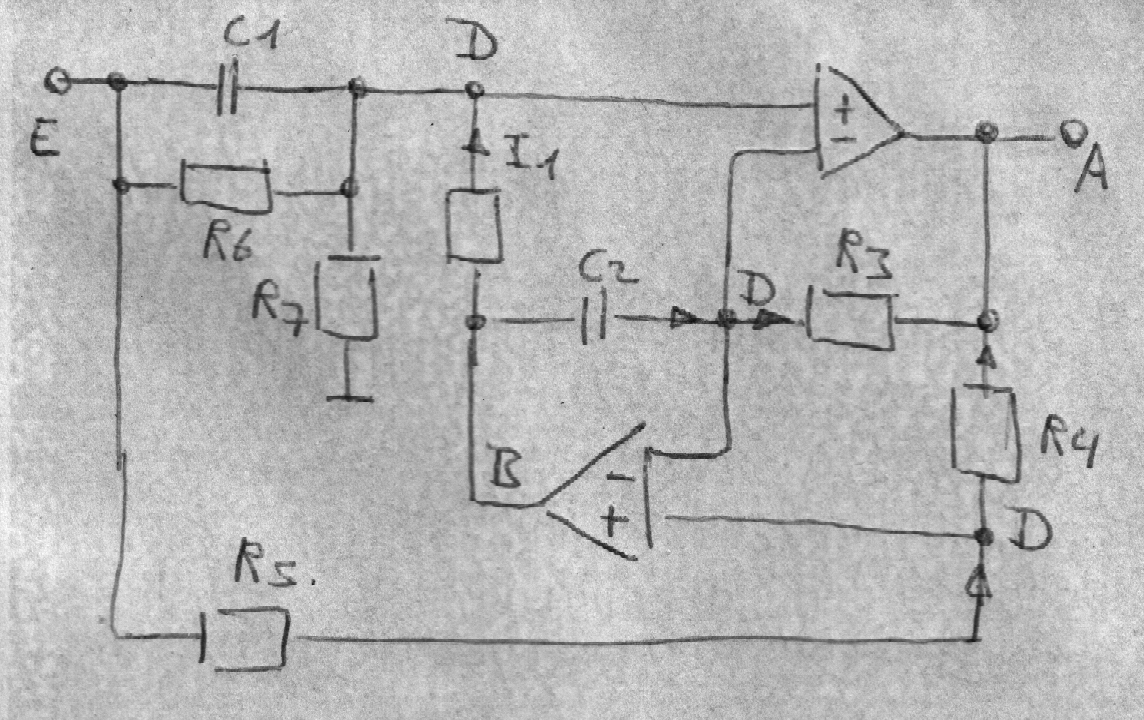
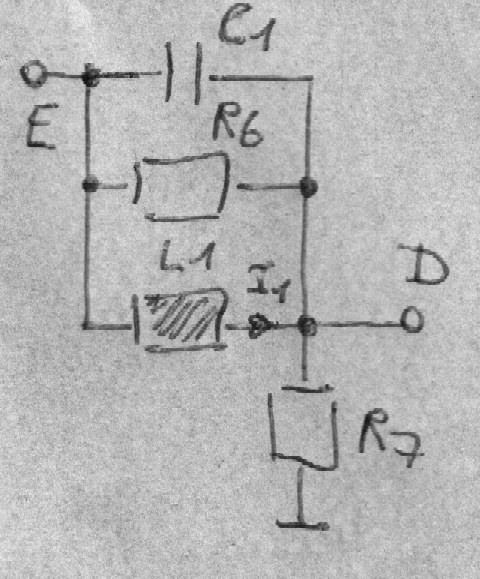
Um zur Induktivität zu gelangen, fange ich bei R₅ an und hangel mich dann bis zu R₁ durch.

(E - D) / R₅ = (D - A) / R₄

(E - D) R₄ / (R₃ R₅) = (D - A) / R₃ = (B - D) jωC₂

(E - D) R₄ / (jωC₂ R₁ R₃ R₅) = (B - D) / R₁ = I₁

Zwischen den Anschlußpunkten D & E befindet sich also die virtuelle induktive Impedanz Z₁.

(E - D) / I₁ = Z₁ = jωC₂ R₁ R₃ R₅ / R₄

Entsprechend ergibt sich folgende Schaltung.

(E - D) (1 / R₆ + jωC₁ + R₄ / (jωC₂ R₁ R₃ R₅) ) = D / R₇

Wenn   R₄ = R₅   und   R₆ = R₇   gesetzt wird, ergibt sich folgendes.

D = E (-ω² R₁ R₃ C₁ C₂ + jω R₁ R₃ C₂ / R₆ + 1)   /   ( -ω² R₁ R₃ C₁ C₂ + 2 jω R₁ R₃ C₂ / R₆ + 1 )

Die Ausgangsspannung A im Verhältnis zur Spannung D ergibt sich aus erster Gleichung folgendes.

A = 2D - E

Beides zusammen gesetzt ergibt.

A / E = (-ω² R₁ R₃ C₁ C₂ + 1)   /   ( -ω² R₁ R₃ C₁ C₂ + 2 jω R₁ R₃ C₂ / R₆ + 1 )

Wobei   T² = R₁ R₃ C₁ C₂   und
2DT = 2 R₁ R₃ C₂ / R₆ → D = 1 / R₆ × √(R₁ R₂ C₂ / C₁ )

Zum Vergleich, eine Bandsperre ist ein PD²T₂-System mit folgender Gleichung.

G(s) = (b₂ s² + 1) / ( a₂ s² + a₁ s + 1 )

Zum Anfang

Quellen

biancahoegel.de   Filter (Elektrotechnik)
changpuak.ch   Fliege Notch Filter
circuitlab.com   Fliege Filter with a virtual ground - Narrow band filter PUBLIC
crbond.com   Filter Algorithms, Parameters and Software for Electronic Circuits
dr-seifert-online.de   NichtinvSallenandKeyTiefHochpass.pdf
hs-karlsruhe.de   PT2-Glied
electronicdeveloper.de   Doppel-T-Filter, Kerbfilter, Notchfilter - Online calculator
electronics-tutorials.ws   Aktiver Tiefpassfilter
elektroniktutor.de   Aktive elektrische Filterschaltungen
fritz.dellsperger.net   Intermodulation Calculator, Zweitore, Filter-Design, etc.
gatech.edu   Discrete_01.pdf - SECOND-ORDER ACTIVE FILTERS
  RCL low-pass, sallen-key, MLF, Tow-Thomas, high-pass
gunthard-kraus.de   Leichter Einstieg in die SPICE-Schaltungssimulation mit LTspice IV oder VII
hinkel-elektronik.de   Elektrotechnik Formelsammlung.pdf
ijdata.com   verkaufen LspCAD
matheplanet.com  
maximintegrated.com   APPLICATION NOTE 1762
  A Beginner's Guide to Filter Topologies
netzmafia.de   Texas_SingleSupply.pdf oder SLOA058.pdf
  summing, difference, simulated inductor, Instrumentation Amplifiers,
  Filter (LP, HP, AP),
  (Sallen-Key, Multiple Feedback, Twin T, Fliege, Akerberg-Mossberg, BiQuad, State Variable)
netzmafia.de   Mikrocontroller, Hardware, PC und Linux
njit.edu   TUTORIAL: Introduction to Filter Design
  Butterworth, Chebyshev, Sallen-Key, Tow-Thomas
numericana.com   Linear Filters - Network Synthesis and Design
kecktaylor.com   Free Analog Filter Program
passific.fr   502af904572be-Polycop Electro-Filtrage - 2012 - Compte.pdf
  Filtrage Analogique - Polytech’Montpellier
rfwireless-world.com   Difference between Butterworth filter vs Chebyshev vs Bessel vs Elliptic filter
sciencedirect.com   Sallen Key
softwaredidaktik.de   Programm Aktiv Filter (nicht gekauft)
studyflix.de   Das PT2-Glied
ti.com   Filter design tool
ti.com   slyt235.pdf - High-speed notch filters
  Twin-T notch filter, Fliege notch filter
ti.com   sloa093.pdf - Filter Design in Thirty Seconds
  LP, HP, BP, BS

Zum Anfang