Auf umliegenden Seiten habe ich…
Spannungsteiler und passive Filter
für div. Verstärker, HP, TP, etc.
allgemeine OP-Schaltungen Addierer, Subtrahierer, etc.
aktive Filter-Schaltungen TP, HP, BP, BS, etc.
spezielle Filter EQ, BiQuad, state variable Filter, Oszillator etc.
Bereits bei den passiven Filter
habe ich Begriffe aus der Regelungstechnik eingeführt.
Anbei ein Beispiel eines allgemeinen Tiefpasses 2. Ordnung
G(s) = b0 / ( a2s2 + a1s + 1 )
Die statische Verstärkungen kann ich darstellen mit
b0 = k .
Die Resonanzfrequenz finde ich wieder in
a2 = T2 = 1 / ω02
und die Dämpfung in
a1 = 2DT = 2D / ω0
Den Begriff Güte oder Gütefaktor kann ich als Verhältnis der
Anfangsenergie (z.B. max. Energie in der Spule) zum Energieverlust innerhalb einer
Periode 1 / f0 = 2π / ω0 beschreiben.
Kurz beschrieben ist das unter wikipedia.org Gütefaktor.
Bei einem Tiefpass 2. Ordnung kann ich auch schreiben…
Q2 = a2 / a12 = T2 / (2DT)2
Somit wird die Güte Q zu: Q = 1 / 2D
Bei Bandpässen gibt es noch eine weitere Definition der Güte Q
über die Bandbreite bei -3dB:
Q = f0 / B-3dB
Bei nahezu allen analogen Filter haben ich, als Antwort auf einen Einheitssprung,
eine, nahezu bis ins unendliche, abklingende Exponential-Funktion.
Aufgrund dieser Antwort, werden diese Filter auch IIR - infinite impulse response - Filter genannt,
wobei es prinzipiell egal ist, ob es sich um einen Einheitssprung oder Impuls handelt.
Digital kann ich diesen Filtertyp ebenso realisieren.
Durch die Rückkopplung ergibt sich eine nahezu unendliche Impulsantwort.
Es ist aber digital auch möglich nicht rückgekoppelte Filter mit einer endlich Antwort zu realisieren.
Diese Filter werden daher FIR - finite impulse response - Filter genannt.
Zum Anfang
Alle
passiven Filter haben eine unendliche Impulsantwort
und gehören dadurch zu den IIR-Filter.
Habe ich Filter 2. Grades, kann ich sie durch ω0 und D beschreiben.
Verschiedene Wissenschaftler haben nun,
je nach Zielsetzung, eine andere Dämpfung D berechnet.
Daraus folgen auch unterschiedliche spezifische Vor- und Nachteile.
Pafnuti Lwowitsch Tschebyschow (1821 - 1894) wollte im Sperrbereich
ein möglichst scharfes Abknicken (Flankensteilheit) erreichen.
Dafür musste er eine gewisse Welligkeit ε (konstanter Amplitude)
im Durchlassbereich (passband) zulassen.
Weitere Nachteile sind ein beträchtliches Überschwingen bei der Sprungantwort
(stärker als beim Butterworth) und eine große Änderung der Gruppenlaufzeit.
Ist die Welligkeit nur im Sperrbereich (stopband) erlaubt,
spricht man vom inversen Tschebyscheff.
Geht die Welligkeit gegen Null, ergibt sich ein Butterworth-Filter.
Details kann man z.B. nachlesen unter…
wikipedia.org Chebyshev filter
eit.hs-karlsruhe.de Tschebyscheff-Filter
deacademic.com Tschebyscheff-Filter
Die allgemeine Übertragungsfunktion eines PT2-Systems lautet:
G(s) = b0 / ( a2s2 + a1s + 1 )
= ( b0 (a2s2 - a1s + 1) )
/ ( (a2s2 + a1s + 1) (a2s2 - a1s + 1) )
= ( b0 (a2s2 + 1 - a1s) )
/ (a22s4 + 2 a2s2 - a12s2 + 1)
Zwecks Normierung an der Stelle G(s = 1) ≈ -3 dB und
b0 = 1 ist das Betragsquadrat
1/2 = ( (1 - a2)2 + a12 )
/ (a22 - 2 a2 + a12 + 1)2
= ( (1 - a2)2 + a12 )
/ ( (1 - a2)2 + a12 )2
→ 2 = (1 - a2)2 + a12
Mit der Bedingung n a2 = a12 und testweise n = 1
ereben sich die gesuchten Koeffizienten zu
a2 = 0,5 + 0,5√5 ≈ 1,618 und
a1 ≈ 1,2720.
Die verschobene Resonanzfrequenz ergib sich aus.
s1,2 = - Dω0 ± ω0 √ ( D2 - 1 )
= - 0,5 / √(0,5 ×(1 + √5)) ± 0,5 j √3
≈ - 0,3931 ± j × 0,8660
Den Realteil in G(s) eingegeben, ergibt…
G(s ≈ 0,3931) ≈ ( √(Re2 + Im2) ) / ( …) ≈ 0,9014 / 0,7590 ≈ 1,1876 ≈ 1,49 dB
Bei gerader Ordnung, ist hier (Amax2 / A02) - 1 = ε2 → ε ≈ 0,6406
Also, prinzipiell bekommt man durch probieren vom Parameter 0 ≤ n ≤ 2 eine Welligkeit ε heraus.
Mit vorgegebenen ε die gewünschten Parameter zu bestimmen, macht,
bei den heutigen Möglichkeiten fertiger Programme, per Hand keinen Sinn mehr…
Da es genügend Programme zur Berechnung gibt,
hier nur ein paar konkrete Beispiele für ein Tschebyscheff-Filter 2. Ordnung.
| Welligkeit | a1 = 2DT | a2 = T2 | Q = √(a2) / a1; D = 1 / 2Q |
|---|---|---|---|
| 3 dB | ≈ 1,0650 | ≈ 1,9305 | Q ≈ 1,305 oder D ≈ 0,3833 |
| 2 dB | ≈ 1,1813 | ≈ 1,7775 | Q ≈ 1,129 oder D ≈ 0,4430 |
| 1,49 dB | ≈ 1,2720 | ≈ 1,6180 | Q = 1 oder D = 0,5 |
| 1 dB | ≈ 1,3022 | ≈ 1,5515 | Q ≈ 0,957 oder D ≈ 0,5227 |
Man muss sich vor Augen führen, dass die damalige Wissenschaft keine Taschenrechner,
sondern lediglich
wikipedia.org Rechenschieber
besass, mit denen sie große Tabellenwerke erstellten.
Zum Anfang
Ähnlich wie Tschebyscheff, haben sich Wilhelm Cauer (1900 - 1945) oder
Yegor Zolotarev (1847 - 1878) mit eliptischen Filter beschäftigt.
Wärend beim Tschebyscheff nur im Durchlassbereich eine Welligkeit ist und im Sperrbereich keine,
ist hier in beiden Breichen die Welligkeit individuell einstellbar.
Im Falle das sie in beiden Bereichen gleich ist, ist die größt mögliche Flankensteilheit gegeben.
Um einen Cauer oder inversen Tschebyscheff zu realisieren, ist bei gleicher Ordnung mehr Aufwand nötig,
als bei den übrigen Filter, da der Nenner nicht mehr nur aus b0 besteht.
G(s) = (… + b0) / ( a2s2 + a1s + 1 )
Stephen Butterworth (1885 - 1958) verfolgte ein anderes Ziel
des möglichst monotonen Amplitudenganges (maximal flach),
sowohl im Durchlass- als auch im Sperrbereich.
Als Folge hat man eine relativ frequenzabhängige Gruppenlaufzeit und
der Phasenverlauf besitzt eine kleine Nichtlinearität.
Dies erkauft man sich mit beträchtlichen Überschwingen bei der Sprungantwort
und einer geringen Flankensteilheit im Übergangsbereich der Bildebene.
Siehe z.B.
calculatoredge.com Sallen-Key Butterworth Low Pass Filter Calculator
G(s) = b0 / ( a2s2 + a1s + 1 ) mit der Bedingung 2 a2 = a12 und 2 = (1 - a2)2 + a12
| Welligkeit | a1 = 2DT | a2 = T2 | Q = √(a2) / a1; D = 1 / 2Q |
|---|---|---|---|
| ε = 0 | √2 ≈ 1,4142 | 1 | Q = D = √(0,5) ≈ 0,707 |
Zum Anfang
Der Legendre-Filter (optimum "L" filter) ist ein Kompromiss zwischen Butterworth und Tschebyscheff
und wurden 1958 von Athanasios Papoulis (1921 - 2002) vorgestellt.
Der Vorteil zum Butterworth ist die höhere Flankensteilheit im Übergangsbereich,
ohne den Nachteil der Welligkeit des Tschebyscheff-Filters.
Da Bilder meist mehr sagen als Worte, anbei eine Seite eines Filter-Software Herstellers…
nuhertz.com Legendre Filters
Friedrich Bessel (1784 1846) hatte sich zum Ziel gesetzt
ein möglichst optimales „Rechteckübertragungsverhalten“ zu erlangen.
Hierfür ist es nötig, eine möglichst konstante Gruppenlaufzeit
(maximally-flat group delay) im Durchlassbereich zu haben.
Ein linearer Phasengang im Durchlassbereich,
führt zu einem geringen Überschwingen bei der Sprungantwort.
Als Preis, hat der Bessel-Filter eine noch flachere Flankensteilheit
im Übergangsbereich als der Butterworth-Filter.
Gelegentlich wird im Zusammenhang mit den Bessel-Filter auch W. E. Thomson genannt.
Wenn ich eine Frequenzweiche (crossover) für Laustsprecherchassis benötige,
trenne ich zunächst die Frequenzen und später interferrieren sich die Schallwellen wieder im Raum.
Bei der Kombination Butterworth Hochpass & Tiefpass
entsteht allerdings im Übergangsbereich eine Anhebung.
Diese unerwünschte Anhebung ist beim Bessel-Filter nicht gegeben,
weswegen sie gerne als "Audio crossover" verwendet werden.
Siehe z.B.
wikipedia.org Bessel filter
ranecommercial.com A Bessel Filter Crossover, and Its Relation to Others
hackaday.com Bessel Filter mit Spice
gist.github.com Bessel Filter mit Python
wikipedia.org Audio crossover
G(s) = b0 / ( a2s2 + a1s + 1 ) mit der Bedingung 3 a2 = a12 und 2 = (1 - a2)2 + a12
| a1 = 2DT | a2 = T2 | Q = √(a2) / a1; D = 1 / 2Q |
|---|---|---|
| ≈ 1,3617 | 0,5 (√(5) - 1) ≈ 0,6180 | Q ≈ 0,5773 oder D ≈ 0,8661 |
Zum Anfang
Das Transitional-Butterworth-Thomson-Filter habe ich nur der Vollständigkeit halber aufgenommen
und ist ein Kompromiss zwischen Butterworth und Bessel-Filter (Thomson-).
Bei der kritischen Dämpfung verhält sich ein System 2. Ordnung,
wie die Hintereinanderschaltung zweier Systeme 1. Ordnung.
Daher ist kein Überschwingen mehr möglich.
Gegenüber dem Bessel-Filter gibt es noch eine beachtliche Verschlechterung des Amplitudenganges.
G(s) = b0 / ( a2s2 + a1s + 1 )
mit der Bedingung D = 1 → 4 a2 = a12
und Amplitude normiert 2 = (1 - a2)2 + a12
| a1 = 2DT | a2 = T2 | Q = √(a2) / a1; D = 1 / 2Q |
|---|---|---|
| ≈ 1,2872 | √(2) - 1 ≈ 0,4142 | Q = 0,5; D = 1 |
Zum Anfang
Filter-Typen wie bei den IIR-Filtern, finde ich bei den FIR-Filtern nicht wieder,
wegen fehlender Rückkopplung.
Finite Impulse Response-Filter sind klassischerweise digital und nicht rückgekoppelt aufgebaut.
Aufgrund dessen wird z.B. ein Einheitsimpuls den Filter nur einmal durchlaufen.
FIR-Filter sind daher auch immer stabil…
Zunächst ein paar Definitionen:
Nun kann man sich ein FIR-Filter vorstellen,
wie eine Eimerkettenschaltung oder kaskadiertes Schieberegister,
an dem an jeden Abgriff das unterschiedlich stark verzögerte Eingangssignal En…En-N
mit einen anderen Koeffizienten b0…bN multipliziert wird.
Die Summe aller Multiplikationen, entspricht dem Ausgangssignal.
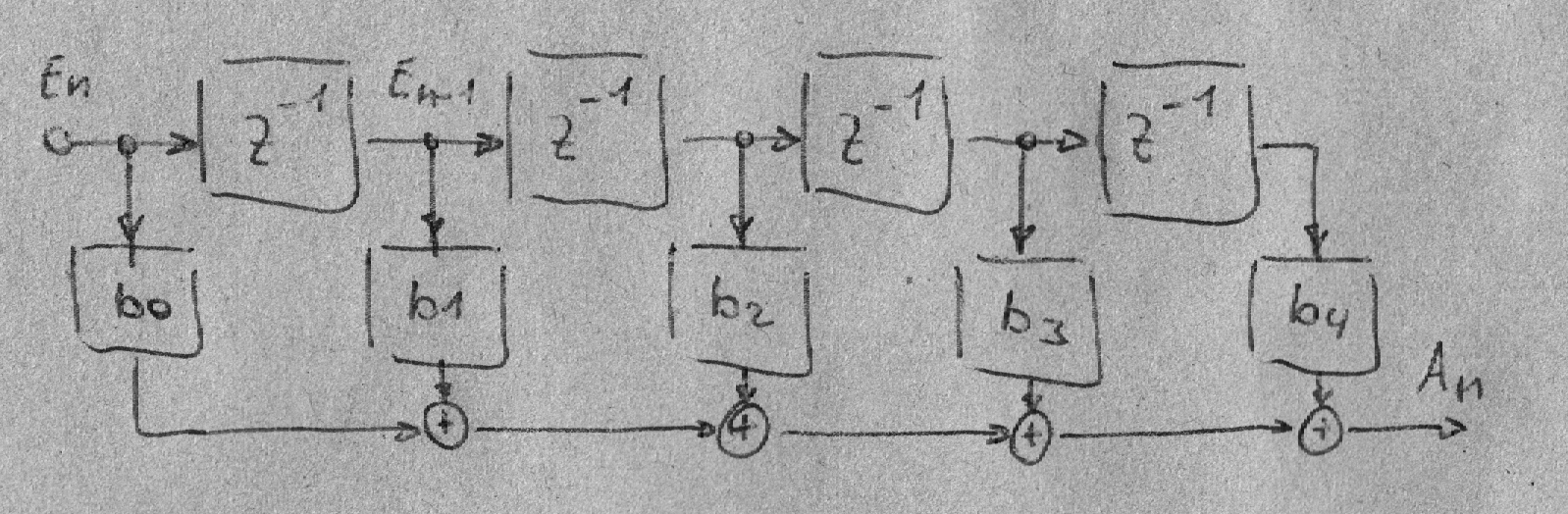
An = En b0 + En-1 b1 + … + En-N bN
Entsprechend, ist die Länge der Impuls-Antwort gleich der Anzahl N+1 an Speicher oder Koeffizienten.
Im Vergleich zum IIR-Filter werden für vergleichbare Wirkung mehr Koeffizienten benötigt.
Das heist es ist eine höhere Ordnung erforderlich,
was mehr Speicherbedarf bedeutet und mehr Multiplikationen mit sich bringt.
Bei symmetrischen Koeffizienten ist das Ausgangs-Signal konstant um die halbe Koeffizientenzahl,
multipliziert mit der Symbolrate verzögert.
Das heisst dieser Filter hat eine konstante Gruppenlaufzeit und ist daher linearphasig.
Da, die Anzahl der Koeffizienten oder die Ordnung begrenzt ist, weicht der reale Filter vom Ideal ab.
Dieses Abschneiden der idealen unendlichen Funktion wird auch Fensterwahl bezeichnet.
Also je nach Fensterwahl (Rectangular, Hamming, Blackman-Harris, Triangular, Kaiser, etc.) komme ich,
bei gegebener Koeffizientenzahl, unterschiedlich gut an das Ideal heran.
Siehe z.B.
itwissen.info FIR-Filter
elprocus.com Know all About FIR Filters in Digital Signal Processing
barrgroup.com digital-filters FIR IIR mit C Beispiel
ti.tuwien.ac.at Digital Signal Processing .pdf Dateien
mathworks.com FIR Filter Design with Matlab
dspguru.com FIR Filter pro & con's
thenucleargeeks.com FIR-filters with python example
wirelesspi.com FIR-filters with Matlab example
t-filter.engineerjs.com Webseite mit Javaprogramm für die Berechnung der FIR-filter Koeffizienten
dsprelated.com SPECTRAL AUDIO SIGNAL PROCESSING
dsprelated.com FIR_Digital_Filter_Design
zone.ni.com nyquist filters (Raised Cosine, half band)
Zum Anfang
Konkretes Beispiel:
Der ADC PCM1807 hat 64 faches Oversampling.
Damit kann der analoge Eingangs-Filter, mit ca. 20 KHz Eckfrequenz, recht einfach (als RC-Glied) ausfallen,
da bei 41 KHz × 64 ≈ 2,6 MHz bereits 2 Dekaden durchstrichen sind.
Das heisst ein mögliches Störsignal hat bei einen einfachen PT1-System nach 2 Dekaden nur noch -40 dB.
Im ADC ist es allerdings dann erforderderlich, mit einen sog. decimation Filter,
auf die Sample-Frequenz von z.B. fs = 44,1 KHz zu gehen.
Ohne das Oversampling müsste der Eingangsfilter wesentlich steilflankiger sein
und wäre damit wesentlich aufwändiger…
Ein Spezialfall der Nyquist-Filter ist der Raised-Cosine-Filter.
Geht die Anzahl der Koeffizienten bei den Raised-Cosine-Filter oder Kosinus-Roll-off-Filter gegen unendlich,
ist die Impulsantwort im Ideal-Fall eine Si-Funktion = sin(x) / x,
was dann im Zeitbereich einem idealen Tiefpass entspricht.
Der Root-Raised-Cosine-Filter ist eine Abwandlung des Raised-Cosine-Filter.
Er ist primär für die Nachrichtentechnik gedacht,
wo man Signale erzeugen möchte, welche möglichst wenig Bandbreite benötigen.
Hier wird also, sowohl im Sender alsauch im Empfänger, das gleiche Filter verwendet.
Zwei RRC-Filter hintereinander wirken also wie ein Raised-Cosine-Filter.
Hier wird statt einer Si-Funktion (positive und negative Polarität)
eine Gauß'sche Glockekurve (nur positiv) angewendet.
Siehe z.B.
de.wikipedia.org Gauß-Filter
en.wikipedia.org Gaussian filter
stein-sw.de filterung gauss-filter
newikis.com/de Gauß-Filter
Zum Anfang
Der Sallen-Key-Filter (IIR) ist eine Schaltung mit einfacher Mitkopplung
von R. P. Sallen und E. L. Key,
welche es ermöglicht mit minimalem schaltungstechnischem Aufwand ein analoges Filter
mit geringer Güte ca. Q < 3 aufzubauen.
Aufgrund der Abzweigstruktur sind keine komplexen Nullstellen möglich,
mit der Folge Bandsperre und Filter mit elliptischen Grundgliedern,
wie beim Cauer-Filter, sind nicht möglich.
Einen Sallen-Key-Filter nutze ich beispielsweise beim Tiefpass 2. Ordnung.
Siehe z.B.
wikipedia.org Sallen-Key-Filter
ti.com Analysis of the Sallen-Key Architecture (Application report.pdf)
analog.com Analysis of the Sallen-Key Filters (Mini Tutorial MT-222.pdf)
sim.okawa-denshi.jp
Sallen-Key low-pass Filter Design Tool
MLF- Filter oder eingedeutscht Filter mit Mfg - Mehrfachgegenkopplung
sind gegenüber Sallen-Key-Filter nicht so anspruchsvoll,
was die Grenzfrequenz des OPs angeht. Daher ist auch eine höhere Güte realisierbar.
Siehe MLF-Tiefpass 2. Ordnung
Siehe z.B.
aktivfilter.de Tiefpass mit Mehrfachgegenkopplung
frankfurt-university.de tiefpass.pdf
spicelab.de
PSpice-Simulation eines aktiven Hochpasses mit Mehrfachgegenkopplung
zhaw.ch
Aktive RC-Filter.pdf
Siegfried Linkwitz (1935 - 2018) und Russ Riley kommen aus den Bereich Lautsprecherbau.
Sie hatten festgestellt, dass die Überlagung von Butterworth Hoch- und Tiefpass Signalen
im Übernahmebereich zu einer Erhöhung führt.
Um die Erhöhung zu vermeiden, haben sie die Dämpfung erhöht.
→ Bessel Q ≈ 0,5774
→ kritische Dämpfung Q = 0,5
Eine Linkwitz-Riley-Frequenzweiche 2. Ordnung hat eine Steilheit von 40 dB je Dekade
und ist damit eine Kombination aus
PT2-Filter
und
D2T2-Filter.
Laut Wiki, werden diese aktiven Filter in Sallen-Key Technologie
mit einer Güte von Q = 0,5 gebaut ???…
Siehe z.B.
de.wikipedia.org Linkwitz-Riley-Filter
musicdsp.org 4th-order Linkwitz-Riley-Filter Liste der Koeffizienten
linkwitzlab.com Linkwitz-Riley-Filter
ranecommercial.com A Bessel Filter Crossover, and Its Relation to Others
wikipedia.org Audio crossover
Zum Anfang
Zum Anfang